前期提示
以下东西纯属个人消化
缘由
首先说一下写这个东西的原因:就是这个卷积公式的理解一直都是我学习信号与系统的拦路虎,一直无法理解这个是什么东西,终于在今晚弄懂了我滴天啊!
卷积公式的形式
首先来看一下这个卷积公式的形式 积分形式
$$(f*g)(n)=\int^{+\infty}_{-\infty}f(\tau)g(n-\tau)d{\tau}$$离散形式
$$(f*g)(n)=\sum^{+\infty}_{-\infty}f(\tau)g(n-\tau)$$翻卷
其实吧,我一直没办法就是为什么那个$f(\tau)$要乘于一个负的$g(n-\tau)$,我认为关键就是理解的这个$-\tau$,理解了这个就理解了整个公式.
举一个例子
扔石头
往水面仍石头,我们把水面的反应当成的一个冲击反应,我们在t=0时,扔下一个石头会激起一个h(0)的波纹,但是水面不会立刻平静,随着时间的流逝,波纹幅度会越来越小,在t=1时刻,幅度衰减为h(1), 在t=2时刻,幅度衰减为h(2)……直到一段时间后,水面重复归于平静.
从时间轴上来看,我们只在t=0时刻丢了一块石头,其它时刻并没有做任何事,但在t=1,2….时刻,水面是不平静的,这是因为过去(t=0时刻)的作用一直持续到了现在。那么,问题来了:如果我们在t=1时刻也丢入一块石子呢?此时t=0时刻的影响还没有消失(水面还没有恢复平静)新的石子又丢进来了,那么现在激起的波浪有多高呢?答案是当前激起的波浪与t=0时刻残余的影响的叠加。那么t=0时刻对t=1时刻的残余影响有多大呢?为了便于说明,接下来我们作一下两个假设:
- 1. 水面对于“单位石块”的响应是固定的.
- 2. 丢一个两倍于的“单位石块”的石块激起的波纹高度是丢一个石块的两倍(即系统满足线性叠加原理)现在我们来计算每一时刻的波浪有多高:
那么我们一个时刻就扔一个石头,t=0,t=1,t=2时,以此类推.那么我们来算一下每个时水面的反应:
y为水面的反应,x为石子,h为水面的激起波澜的函数
-
t=0时: y(0)=x(0)*h(0)//t0时刻一个石子在h0时刻激起y0
-
t=1时 y(1)=x(1)*h(0)+x(0)*h(1)//这个就是当前石子激起h(0),和之前那个x(0)那个的残余的叠加
-
t=2时: y(2)=x(2)*h(0)+x(1)*h(1)+x(0)*h(2)
以此类推
- t=n 时: y(n)=x(n)*h(0)+x(n-1)*h(1)+x(n-2)*h(2)+…+x(0)*h(n)
推到这一步把用累加符号弄在一起你会惊讶的发现,我擦这个不就是说这个吗? $\sum_{i=0}^nx(i)h(n-i)$是不是很是相像$(fg)(n)=\sum^{+\infty}_{-\infty}f(\tau)g(n-\tau)$.这就是离散卷积的公式了理解了上面的问题,下面我们来看看“翻转”是怎么回事:当我们每次要丢石子时,站在当前的时间点,系统的对我们的回应都是h(0),时间轴之后的(h(1),h(2)…..)都是对未来的影响。而整体的回应要加上过去对于现在的残余影响。现在我们来观察t=4这个时刻.
- 站在t=0时刻看他对于未来(t=4)时刻(从现在往后4秒)的影响,可见是x(0)*h(4)
- 站在t=1时刻看他对于未来(t=4)时刻的影响(从现在往后3秒),可见是x(1)*h(3)
- 站在t=2时刻看他对于未来(t=4)时刻的影响(从现在往后2秒),可见是x(2)*h(2)
- 站在t=3时刻看他对于未来(t=4)时刻的影响(从现在往后1秒),可见是x(3)*h(1)
图示:
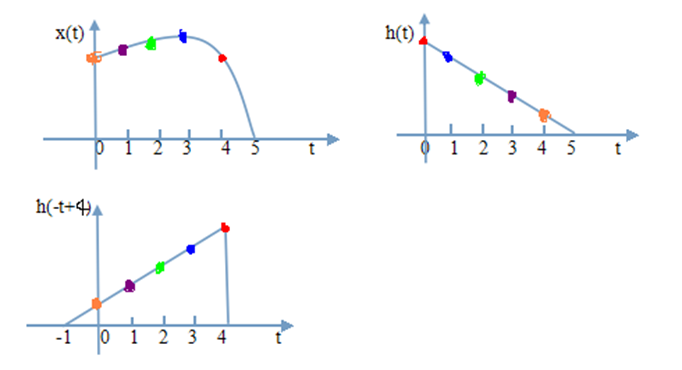
你将第一幅和第三幅对应的乘起来是不是就是那个 y(4)=x(4)*h(0)+x(3)*h(1)+x(2)*h(2)+x(1)*h(3)+x(0)*h(4)